Multivariable Calculus

• The set of points in ${\mathbb{R}}^2$ defined by $\{(x,y)\mid y=f(x)\}$ is called the graph of the function $f:\mathbb{R}\to \mathbb{R}$.

• The set of points in ${\mathbb{R}}^3$ defined by $\{(x,y,f(x,y))\mid (x,y)\in {\mathbb{R}}^2\}$ is called the graph of the function $f:{\mathbb{R}}^2\to \mathbb{R}$.

• Let $f:{\mathbb{R}}^2\to \mathbb{R}$ be a two-variable function, and $C\in \mathbb{R}$, the set of points defined by $\{(x,y)\mid f(x,y)=C\}$ is called the level curve of $f$ at the level $C$.

• $\underset{p\to p_0}{\lim }f(p)=L⟺\forall \epsilon >0,\exists \delta >0:(0<d(p,p_0)<\delta ⟹|f(p)-L|<\epsilon )$.

• Let $f(x,y)$ be a real-valued function of two variables defined on an neighborhood of the point $(x_0,y_0)$.

  • The function $f$ is said to be continuous at the point $(x_0,y_0)$ if $\underset{(x,y)\to (x_0,y_0)}{\lim }f(x,y)=f(x_0,y_0)$. (assuming the limit exists)
  • Partial Derivatives
    • The partial derivative of $f$ with respect to $x$ at the point $(x_0,y_0)$ is defined as $\frac{\partial f}{\partial x}(x_0,y_0)=\underset{h\to 0}{\lim }\frac{f(x_0+h,y_0)-f(x_0,y_0)}{h}$. (assuming the limit exists)
    • The partial derivative of $f$ with respect to $y$ at the point $(x_0,y_0)$ is defined as $\frac{\partial f}{\partial y}(x_0,y_0)=\underset{h\to 0}{\lim }\frac{f(x_0,y_0+h)-f(x_0,y_0)}{h}$. (assuming the limit exists)
    • $\frac{{\partial }^{2}f}{\partial x\partial y}=\frac{\partial }{\partial x}\left(\frac{\partial f}{\partial y}\right)$
  • The directional derivative of $f$, in the direction of the vector $\mathbf{v}=(a,b)$, in the point $p_0=(x_0,y_0)$, is defined as $D_{\mathbf{v}}f(p_0)=\underset{t\to 0}{\lim }\frac{f(p_0+tv)-f(p_0)}{t}$.
    • (Assuming the limit exists)
    • Also denoted by $\frac{\partial f}{\partial \mathbf{v}}(p_0)$

• Let $f(x,y)$ be a function of two variables, defined in a neighborhood of $p_0=(x_0,y_0)$.

  • $f$ is said to be differentiable at $p_0$ if there exist $A,B\in \mathbb{R}$ and function $r(x,y)$ such that:
    • $\forall (x,y)\in \text{dom}(f),f(x,y)=f(x_0,y_0)+A(x-x_0)+B(y-y_0)+r(x,y)$
    • $r(p)=o(d(p,p_0))$ in the neighborhood of $p_0$

Multiple Integrals

double integral

• The double integral of a function $f(x,y)$ over a region $D$ in the $xy$-plane is defined as ${\iint }_{D}f(x,y)dxdy=\underset{m,n\to \infty }{\lim }\sum _{i=1}^m\sum _{j=1}^{n}f(x_{ij},y_{ij})\Delta A_{ij}$, where:
  • $\Delta A_{ij}$ is the area of the rectangle $R_{ij}$
  • $(x_{ij},y_{ij})$ is a point in the rectangle $R_{ij}$.
• If $D$ is a rectangle $[a,b]\times [c,d]$, then the double integral can be evaluated as ${\iint }_{D}f(x,y)dxdy={\int }_a^b{\int }_c^{d}f(x,y)dydx={\int }_c^d{\int }_a^{b}f(x,y)dxdy$.

triple integral

• ${\iiint }_{D}f(x,y,z)dxdydz$

Line Integrals

Line integral of a scalar field

(source: commons.wikimedia.org)

• ${\int }_{\mathcal{C}}f(x,y)ds={\int }_a^{b}f(\mathbf{r}(t))|{\mathbf{r}}^{\prime }(t)|dt$ is the line integral of a scalar field $f$ along a curve $\mathcal{C}$, where:
  • $f:U\to \mathbb{R}$
  • $U\subset {\mathbb{R}}^2$ is an open set
  • $\mathcal{C}\subset U$ is a piecewise smooth curve parametrized by $\mathbf{r}(t)=(x(t),y(t))$ for $t\in [a,b]$.
  • $ds=\sqrt{{\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2}dt$ is the differential arc length along the curve $\mathcal{C}$.

this can be generalized to curve $\mathcal{C}\subset U\subset {\mathbb{R}}^3$ as follows: ${\int }_{\mathcal{C}}f(x,y,z)ds={\int }_a^{b}f(\mathbf{r}(t))|{\mathbf{r}}^{\prime }(t)|dt$ where $\mathbf{r}(t)=(x(t),y(t),z(t))$ for $t\in [a,b]$.

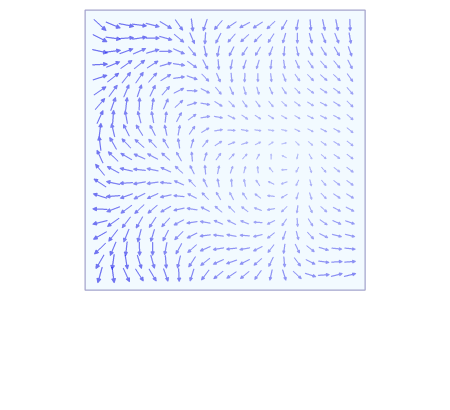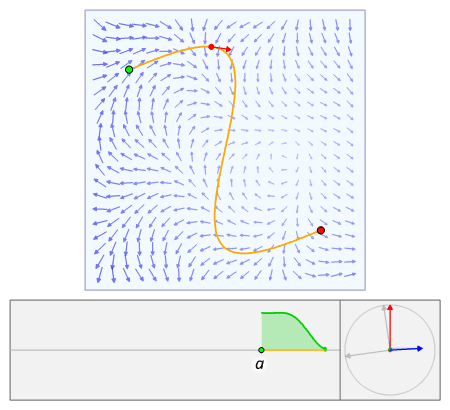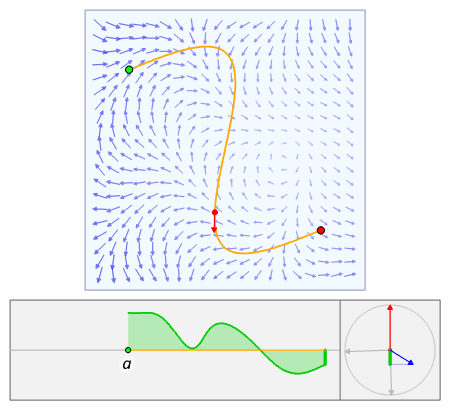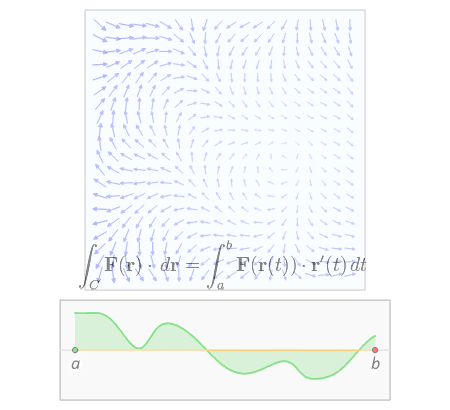
Line integral of a vector field

(source: commons.wikimedia.org)

• ${\int }_{\mathcal{C}}\mathbf{F}(\mathbf{r})\cdot d\mathbf{r}={\int }_a^b\mathbf{F}(\mathbf{r}(t))\cdot {\mathbf{r}}^{\prime }(t)dt$ is the line integral of a vector field $\mathbf{F}$ along a curve $\mathcal{C}$, where:
  • $\mathbf{F}:U\to {\mathbb{R}}^2$
  • $U\subset {\mathbb{R}}^2$ is an open set
  • $\mathcal{C}\subset U$ is a piecewise smooth curve parametrized by $\mathbf{r}(t)=(x(t),y(t))$ for $t\in [a,b]$.
  • $d\mathbf{r}=\left(\frac{dx}{dt},\frac{dy}{dt}\right)dt$ is the differential displacement vector along the curve $\mathcal{C}$.

this can be generalized to curve $\mathcal{C}\subset U\subset {\mathbb{R}}^3$ where $\mathbf{F}:U\to {\mathbb{R}}^3$ and $\mathbf{r}(t)=(x(t),y(t),z(t))$ for $t\in [a,b]$.

Surface Integrals

Surface integral of a scalar field

• (surface given parametrically) Given $S$ is a smooth surface parametrized by $\mathbf{r}(u,v)=(x(u,v),y(u,v),z(u,v))$ for $(u,v)\in D\subset {\mathbb{R}}^2$.
  • The surface integral of a $f$ over $S$ is ${\iint }_{S}f(x,y,z)dS={\iint }_{D}f(\mathbf{r}(u,v))\Vert \frac{\partial \mathbf{r}}{\partial u}\times \frac{\partial \mathbf{r}}{\partial v}\Vert dudv$, where:
    • $f$ is continuous function defined on $S$
    • $dvdu$ is the differential area element on $D$
    • $\frac{\partial \mathbf{r}}{\partial u}\times \frac{\partial \mathbf{r}}{\partial v}$ is the normal vector to the surface $S$ at the point $\mathbf{r}(u,v)$
    • $\Vert \frac{\partial \mathbf{r}}{\partial u}\times \frac{\partial \mathbf{r}}{\partial v}\Vert$ is equal to the area of the parallelogram formed by the tangent vectors $\frac{\partial \mathbf{r}}{\partial u}$ and $\frac{\partial \mathbf{r}}{\partial v}$ at the point $\mathbf{r}(u,v)$.
    • $dS=\Vert \frac{\partial \mathbf{r}}{\partial u}\times \frac{\partial \mathbf{r}}{\partial v}\Vert dudv$ is the differential area element on the surface $S$.
• (surface given implicitly) Given $S$ is a smooth surface defined implicitly by $F(x,y,z)=c$.todo

Surface integral of a vector field

• (surface given parametrically) Given $S$ is a smooth surface parametrized by $\mathbf{r}(u,v)=(x(u,v),y(u,v),z(u,v))$ for $(u,v)\in D\subset {\mathbb{R}}^2$.
  • The surface integral of a vector field $\mathbf{F}$ over $S$ is ${\iint }_S\mathbf{F}\cdot d\mathbf{S}={\iint }_D\mathbf{F}(\mathbf{r}(u,v))\cdot ({\mathbf{r}}_u\times {\mathbf{r}}_v)dudv$, where:
    • $\mathbf{F}$ is continuous vector field defined on $S$
    • $dvdu$
    • ${\mathbf{r}}_u\times {\mathbf{r}}_v=\frac{\partial \mathbf{r}}{\partial u}\times \frac{\partial \mathbf{r}}{\partial v}$
    • $d\mathbf{S}=\left({\mathbf{r}}_u\times {\mathbf{r}}_v\right)dudv$
    • $dS=\Vert {\mathbf{r}}_u\times {\mathbf{r}}_v\Vert dudv$
    • $\hat{\mathbf{n}}=\frac{{\mathbf{r}}_u\times {\mathbf{r}}_v}{\Vert {\mathbf{r}}_u\times {\mathbf{r}}_v\Vert }$ is the unit normal vector to the surface $S$ at the point $\mathbf{r}(u,v)$
    • $\mathbf{F}\cdot \hat{\mathbf{n}}$ is the component of the vector field $\mathbf{F}$ normal to the surface $S$ at the point $\mathbf{r}(u,v)$.
    • The integral also called the flux of $\mathbf{F}$ across $S$, denoted by $\Phi ={\iint }_S\mathbf{F}\cdot \hat{\mathbf{n}}dS$.
      • $\frac{d\Phi }{dS}=\mathbf{F}\cdot \hat{\mathbf{n}}$ is the called flux density of $\mathbf{F}$ across $S$

Stokes’ Theorem

• ${\iint }_S(\nabla \times \mathbf{F})\cdot d\mathbf{S}={\oint }_{\partial S}\mathbf{F}\cdot d\mathbf{r}$ where:
  • $S$ is a smooth oriented surface with boundary $\partial S$
  • $\mathbf{F}$ is a vector field defined on an open region containing $S$
  • $\nabla \times \mathbf{F}$ is the curl of $\mathbf{F}$
  • $d\mathbf{S}$ is the vector area element of $S$
  • $d\mathbf{r}$ is the differential displacement vector along the boundary $\partial S$